Trong phân tích định lượng bằng hồi quy, chúng ta vẫn có thể lượng hóa ảnh hưởng của các biến thuộc tính không có biểu hiện trực tiếp bằng các con số đến giá trị của một biến số khác. Bài viết trình bày cách thức tiến hành hồi quy với biến độc lập là biến thuộc tính (thường gọi là biến giả), và ví dụ ứng dụng trong nghiên cứu thực tế.

I. BIẾN GIẢ

Một vấn đề cơ bản trong phân tích hồi quy là các biến số đưa vào trong mô hình phải được lượng hóa bằng các con số. Tuy nhiên trong thực tế, có nhiều biến số kinh tế có mối quan hệ với rất nhiều các yếu tố trong đó có những biến số không có biểu hiện trực tiếp bằng các con số. Ví dụ, hiệu quả sản xuất kinh doanh của các doanh nghiệp không chỉ phụ thuộc vào quy mô vốn, quy mô lao động trong doanh nghiệp mà còn phụ thuộc vào lĩnh vực sản xuất kinh doanh. Năng suất cây trồng không chỉ phụ thuộc vào khối lượng phân bón mà còn phụ thuộc vào chất lượng giống… Như vậy, làm thế nào để lượng hóa được ảnh hưởng của các đặc điểm không có biểu hiện bằng con số đến giá trị của biến phụ thuộc? Trong phân tích hồi quy, việc sử dụng các biến số đại diện cho các đặc điểm chất lượng như vậy được gọi là kỹ thuật biến giả.

      Như vậy, biến giả trong phân tích hồi quy là các biến chất lượng, không có biểu hiện trực tiếp bằng các con số. Mục đích của việc sử dụng biến giả trong phân tích hồi quy nhằm thể hiện tác động của biến chất lượng đến biến phụ thuộc, so sánh giá trị biến phụ thuộc giữa các mức độ biểu hiện của biến chất lượng…và nhằm một số mục đích khác sẽ được trình bày trong nội dung bài nghiên cứu sau đây.

II. SỬ DỤNG BIẾN GIẢ TRONG PHÂN TÍCH HỒI QUY (REGRESSION WITH DUMMIES)

1. Xây dựng biến giả

Như đã trình bày, các biến chất lượng không có biểu hiện bằng các con số. Vậy làm thế nào để biến chúng thành các biến số số lượng?

Biến giả (Dummies) là các biến chất lượng mà giá trị của chúng chỉ nhận một thuộc tính nào đó. Cho nên, nếu biến giả nhận một thuộc tính nào đó, chúng ta gán giá trị cho biến giả là 1 và nhận giá trị là 0 nếu ngược lại. Nói như vậy có nghĩa là, các biến giả đưa vào phân tích hồi quy chỉ nhận một trong hai giá trị là 1 hoặc 0. Tuy nhiên, một biến giả có thể có nhiều biểu hiện, ví dụ các doanh nghiệp phân theo ngành kinh tế có rất nhiều loại. Như vậy, làm thế nào để gán giá trị thể hiện các loại hình doanh nghiệp trong khi chúng ta khẳng định biến giả chỉ nhận 1 trong hai giá trị đã nêu?

            Giả sử Công ty X đang sử dụng 3 nhóm lao động có trình độ tay nghề khác nhau. Nhóm lao động thứ nhất có trình độ từ phổ thông đến dưới đại học, nhóm thứ hai có trình độ đại học và nhóm thứ ba có trình độ sau đại học. Công ty đang cân nhắc việc trả lương theo năng suất lao động của công nhân. Công ty có số liệu về năng suất lao động của các công nhân trong một thời kỳ. Tuy nhiên, họ muốn có một cơ sở chắc chắn cho việc so sánh năng suất lao động của hai nhóm công nhân, từ đó có chính sách tiền công hợp lý hơn. Vấn đề trên giải quyết như sau:

            + Xác định số biến giả đưa vào mô hình

Số biến giả đưa vào mô hình bằng số biểu hiện của biến thuộc tính trừ đi 1. Giả sử biến thuộc tính muốn đưa vào mô hình có k biểu hiện, số biến giả đưa vào mô hình sẽ là (k – 1) biến.

Với ví dụ trên, số biến chất lượng “Trình độ của lao động” có 3 biểu hiện là dưới đại học, đại học và sau đại học. Vậy số biến đưa vào mô hình sẽ là (3 – 1) biến giả.

            + Gán giá trị cho biến giả

Mức năng suất trung bình của ba nhóm lao động có thể được trình bày dưới dạng hàm hồi quy sau:

                                    Y_i = β₀ + Σβ_jX_ji + a₁D₁ + a₂D₂ + U_i                                               (1)

            Trong đó Y_i là năng suất lao động của công nhân thứ i; X_j là các biến số lượng có ảnh hưởng đến năng suất như kinh nghiệm công tác, độ tuổi… D₁, D₂ là hai biến giả đại diện cho trình độ của lao động và U_i là sai số ngẫu nhiên hàm hồi quy.

Cách gán giá trị cho biến giả D₁ và D₂  như sau:

                D₁ = 1 nếu người lao động có trình độ đại học

D₁ = 0 nếu lao động có trình độ khác

D₂ = 1 nếu lao động có trình độ sau đại học

D₂ = 0 nếu lao động có trình độ khác.

Như vậy chúng ta dễ dàng nhận thấy rằng, nếu cả hai biến D₁ và D₂ đồng thời bằng 0, người lao động có trình độ dưới đại học. Khi đó phạm trù “Dưới đại học” được gọi là phạm trù cơ sở hay thuộc tính cơ sở.

Minh họa cho việc tạo và gán giá trị cho biến giả trường hợp trên như sau:

Như vậy, phạm trù “Dưới đại học” được gọi là phạm trù cơ sở. Mọi so sánh về năng suất lao động giữa các nhóm căn cứ vào kết quả hồi quy là so sánh với nhóm có trình độ dưới đại học.

Cách minh họa như trên giúp chúng ta dễ dàng nhận thức về cách gán giá trị cho biến giả và sắp xếp thông tin trong file dữ liệu đưa vào phần mềm phân tích hồi quy.

2. Ước lượng hệ số của các biến giả và ý nghĩa các hệ số hồi quy

+ Ước lượng các hệ số hồi quy của  biến giả

Việc ước lượng các hệ số hồi quy trong mô hình phân tích hồi quy với biến giả hoàn toàn giống với phương pháp ước lượng sử dụng cho mô hình các biến lượng. Tức chúng ta vẫn sử dụng phương pháp bình phương bé nhất OLS. Với số liệu chúng ta thu thập được về các biến số, chúng ta có thể tiến hành hồi quy bằng chương trình hồi quy tuyến tính (Linear Regression ) trên SPSS, LIMDEP, STATA, EVIEW hoặc trên EXcel.

Sau khi ước lượng mô hình (1) bằng phương pháp bình phương bé nhất, chúng ta thu được các ước lượng đối với các tham số β và a. Khi đó chúng ta có thể biết được năng suất lao động giữa các nhóm trình độ khác nhau có chênh lệch nhau hay không.

Từ mô hình hồi quy (1) thu được sau khi ước lượng, chúng ta có thể thấy:

E(Y/D₁ = 1, D₂ = 0) = β₀ + Σβ_jX_ji + a₁ :                                                                 (2)

                  năng suất lao động trung bình của người có trình độ Đại học

E(Y/D₁ = 0, D₂ = 1) = β₀ + Σβ_jX_ji + a₂ :                                                                 (3)

năng suất lao động trung bình của người có trình độ sau ĐH

E(Y/D₁ = 0, D₂ = 0) = β₀ + Σβ_jX_ji :                                                                          (4)

năng suất lao động trung bình của người có trình độ dưới ĐH

+ Ý nghĩa của hệ số hồi quy riêng (a) của biến giả

            Từ (2), (3) và (4) chúng ta thấy rằng:

                                                                        (2) – (4) = a₁

                                                                        (3) – (4) = a₂

Như vậy, các hệ số a₁ và a₂ thể hiện sự khác biệt về mức năng suất lao động bình quân giữa nhóm lao động có trình độ đại học và sau đại học so với năng suất lao động bình quân của nhóm có trình độ dưới đại học.

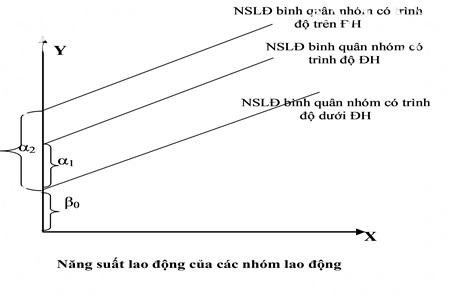
Minh họa kết quả hồi quy (2), (3) và (4) lên đồ thị như sau :

                 Một lưu ý đối với các hệ số hồi quy của biến giả là nó cho biết sự khác biệt về giá trị trung bình biến phụ thuộc là năng suất lao động giữa các nhóm có trình độ học vấn khác so với nhóm có trình độ dưới đại học. Và như vậy, sự khác biệt trong mô hình hồi quy giữa các nhóm là khác biệt ở hệ số chặn của mô hình. Do đó, như đồ thị đã chỉ ra, các đường hồi quy về năng suất lao động của các nhóm song song với nhau. Điều đó ngụ ý rằng, năng suất lao động bình quân giữa các nhóm khác nhau, tuy nhiên mức độ tăng năng suất lao động là như nhau.

Trong trường hợp chúng ta muốn so sánh về năng suất lao động giữa 2 nhóm có trình độ đại học và sau đại học, chúng ta phải xây dựng một mô hình khác để phân tích, hoặc sử dụng phương pháp kiểm định khác.

 3. Kiểm định giả thiết thống kê về hệ số hồi quy của biến giả

Căn cứ vào kết quả hồi quy, chúng ta khẳng định rằng các hệ số a thể hiện sự khác biệt về năng suất lao động bình quân giữa các nhóm so với nhóm có trình độ dưới đại học. Với bất kỳ một bộ số liệu nào khi đưa vào mô hình phân tích hồi quy, chúng ta đều thu được các ước lượng của hệ số hồi quy. Tuy nhiên, liệu có sự khác biệt nào có ý nghĩa thống kê về năng suất lao động giữa các nhóm công nhân khác so với nhóm có trình độ dưới đại học hay không ? Hay nói cách khác, liệu đại đa số lao động có trình độ cao hơn sẽ có năng suất lao động cao hơn nhóm có trình độ dưới đại học ? Để kiểm tra giả thiết này, chúng ta tiến hành kiểm định giả thiết thống kê về các hệ số hồi quy.

+ Kiểm định sự khác biệt về năng suất lao động bình quân giữa nhóm có trình độ đại học so với nhóm dưới đại học :

            - Giả thiết :        H₀ :       a₁ = 0 : NSLĐ hai nhóm có trình độ ĐH và dưới ĐH là như nhau

                                      H₁ :       a₁ ¹ 0 : NSLĐ hai nhóm trên là khác nhau.

            - Tiêu chuẩn kiểm định : Chúng ta sử dụng tiêu chuẩn kiểm định T (T test)

	a1 T=        ---------                ~ ta(n-k-2)              Se(a1)

 

(5)

                                                                                                                     

 

- Quy tắc kết luận:

|T| > t_α/2(n – k-2): Bác bỏ giả thiết H₀, hay nói cách khác, không có cơ sở để khẳng định rằng năng suất lao động hai nhóm nghiên cứu là như nhau.

|T| £ t_α/2(n – k-2) : Chấp nhận giả thiết cho rằng năng suất lao động hai nhóm có trình độ đại học và dưới đại học là như nhau.

+ Kiểm định sự khác biệt về năng suất lao động giữa nhóm có trình độ trên đại học so với nhóm dưới đại học:

- Giả thiết :        H₀ :       a₂ = 0 : NSLĐ nhóm có trình độ trên ĐH và dưới ĐH là như nhau

                                          H₁ :       a₂ ¹ 0 : NSLĐ hai nhóm trên là khác nhau.

            - Tiêu chuẩn kiểm định : Chúng ta sử dụng tiêu chuẩn kiểm định T (T test)

	a2 T =    -----------       ~ ta(n-k-2)             Se(a2)

 

(6)

                       

                                                                                                                    

- Quy tắc kết luận:

|T| > t_α/2(n – k-2): Bác bỏ giả thiết H₀, hay nói cách khác, không có cơ sở để khẳng định rằng năng suất lao động hai nhóm nghiên cứu là như nhau.

|T| £ t_α/2(n – k-2) : Chấp nhận giả thiết cho rằng năng suất lao động hai nhóm có trình độ trên đại học và dưới đại học là như nhau.

III. KẾT LUẬN

Phân tích hồi quy là phương pháp phân tích định lượng các mối quan hệ kinh tế, được sử dụng rộng rãi trong nghiên cứu kinh tế. Nhiệm vụ của phân tích hồi quy bao gồm kiểm tra các giả thiết về các mối quan hệ, ước lượng giá trị trung bình biến phụ thuộc khi đã biết giá trị các biến độc lập, và tiến hành chức năng dự báo. Sử dụng thông tin từ kết quả hồi quy, cho phép chúng ta nhận định đúng đắn về mối quan hệ giữa các biến số kinh tế với nhau, từ đó có căn cứ khoa học cho việc đưa ra các quyết định quản lý phù hợp.

Các biến số đưa vào mô hình phân tích hồi quy phải có biểu hiện bằng con số. Tuy nhiên, chúng ta có thể đưa các biến thuộc tính vào mô hình hồi quy để thực hiện 3 nhiệm vụ cơ bản của phân tích hồi quy. Các biến chất lượng đưa vào mô hình bằng cách thức mã hóa như đã trình bày gọi là biến giả (Dummies). Mục tiêu của sử dụng biến giả trong phân tích hồi quy là kiểm tra mối quan hệ giữa biến phụ thuộc và một biến thuộc tính nào đó, so sánh giá trị trung bình của biến phụ thuộc giữa các biểu hiện khác nhau của biến thuộc tính. Ngoài ra, việc sử dụng biến thuộc tính như đã trình bày, còn có tác dụng tạo ra các biến số tương tác nhằm thể hiện mức độ tác động tổng hợp giữa biến thuộc tính và một số biến độc lập là các biến chất lượng đến giá trị biến phụ thuộc.

Ứng dụng kỹ thuật biến giả trong phân tích hồi quy có nhiều ứng dụng thực tế. Sử dụng tốt kỹ thuật này, chúng ta hoàn toàn có thể kiểm tra được các giả thiết đặt ra đối với mối quan hệ kinh tế giữa một biến số số lượng và biến thuộc tính. Đồng thời, việc so sánh mức độ trung bình của một biến số giữa các biểu hiện khác nhau của cùng một tiêu thức chất lượng giúp chúng ta nhận thức đúng đóng góp của từng nhân tố vào kết quả của biến số lượng, đánh giá đúng xu hướng biến động và từ đó đề xuất các giải pháp thúc đẩy phù hợp.

Tài liệu tham khảo:

[1]. Nguyễn Quang Dong (2013), Bài giảng Kinh tế lượng, NXB Giao thông vận tải, Hà Nội.

[2]. Nguyễn Quang Dong (2013, Giáo trình Kinh tế lượng, NXB Đai học Kinh tế quốc dân, Hà Nội.